En prácticamente cualquier situación de interés en la ciencia y en la ingeniería hay cantidades cuyo valor cambia con el tiempo a las cuales denominaremos variables. Uno de los problemas básicos del Cálculo lo es el de determinar la magnitud de cada uno de esos cambios, así como la razón existente entre los
correspondientes a dos variables cualesquiera.
Percibimos que una variable cambia cuando su valor es distinto en dos momentos determinados, es decir, por el cambio de su valor en el tiempo. Podemos decir que la variación del tiempo, y por lo tanto el cambio en el valor del tiempo, es lo que nos permite advertir cambios en las otras cantidades variables. “Todo cambia” conforme pasa (cambia) el tiempo.
En fin, tenemos que la magnitud del cambio de una cantidad variable es la diferencia entre los valores de la variable, correspondientes a dos momentos determinados. Si lo que interesa es determinar tales cambios (y la razón entre dos cualesquiera de ellos), cuando estos ocurren en un intervalo infinitamente
pequeño (de tiempo), estamos hablando entonces de cambios instantáneos o infinitesimales. Cada uno de estos cambios infinitesimales será llamado diferencial y este será el concepto básico del Cálculo Diferencial.
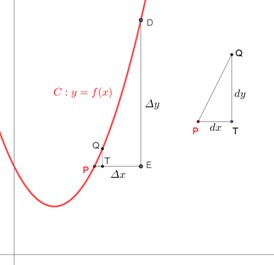
Incremento y Diferencial
Los conceptos de cambio y razón de cambio son sumamente importantes en las ciencias básicas y de la ingeniería. El cambio o incremento de una cantidad variable no es más que la diferencia entre dos de sus valores, esto es, el valor “nuevo” menos el original, mientras que una razón de cambio es el cociente de
dos de tales incrementos.
Ahora bien, con frecuencia interesará conocer cómo están relacionados los cambios de las distintas variables que intervienen en un fenómeno, particularmente para hacer predicciones con un grado aceptable de certidumbre de lo que ocurrirá con el valor de alguna variable en particular (variable dependiente o función), sabiendo o suponiendo cómo cambiará el valor de otra de ellas (variable independiente o simplemente variable).
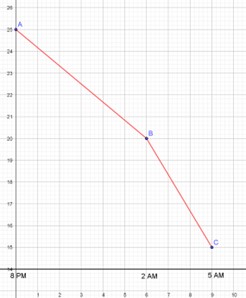
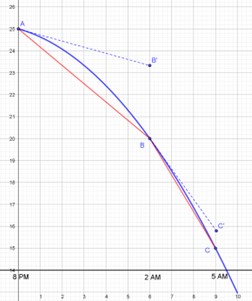
Esto puede hacerse con relativa facilidad cuando se conoce la regla de correspondencia entre las variables de interés, ya que en tal caso sólo hay que evaluar la función en los puntos de interés y calcular la diferencia. Sin embargo, hay situaciones durante el proceso de modelación de un fenómeno, o cuando la información disponible es, por ejemplo, una tabla de valores en que no se conoce la regla de correspondencia. En tales casos resulta sumamente útil poder estimar la magnitud del incremento de la función a partir de la magnitud del incremento de la variable y de la información disponible en el “punto de partida”, es decir, de lo que se conoce de la función para el valor original o inicial de la variable, como el valor de la función o la rapidez con la que cambia su valor en ese punto.
PW_3 Incremento y diferencial.pdf
El asunto de la recta tangente
El esquema curricular, presente en las escuelas de ingeniería de Latinoamérica, comenzó a instrumentarse a mediados del siglo XX. Según este esquema, el currículo se presenta en tres etapas: Ciencias Básicas, Ciencias de la Ingeniería e Ingeniería Aplicada. Además, dentro de ese primer bloque de materias, el de las Ciencias Básicas, muy probablemente aparezcan, primeramente, los cursos de Matemáticas y luego los de Física (y, tal vez, Química o Biología). Esto obliga a que los cursos de Matemáticas se presenten de manera totalmente descontextualizada de las Ciencias de la Ingeniería e, incluso, de la Física básica.
De esta manera, si en el primer curso de Cálculo se quieren utilizar ejemplos que sean comprensibles a los estudiantes, tendrán que plantearse en el contexto de situaciones ya abordadas, desde el bachillerato. Por tal motivo, en el caso de la derivada, la “aplicación” generalmente utilizada es la de la recta tangente, ya que este concepto es abordado desde el bachillerato, o incluso desde la enseñanza básica.
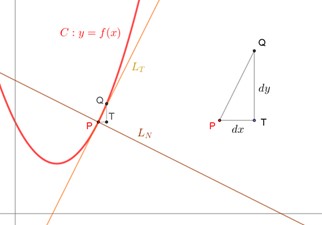
Razón de cambio y función derivada
Para comenzar a hablar de la razón de cambio podemos referirnos, por ejemplo, a la rapidez con la que se mueve un automóvil cuando recorre una carretera. Así, si recorrió una carretera entre dos ciudades, de 60 km de longitud, en un tiempo de 40 minutos, es decir, en 2/3 de hora, diremos que se movió con una velocidad media (o promedio) de km/h, lo que quiere decir que, si se hubiera desplazado con velocidad constante, esta tuvo que haber sido de 90 km/h, y que, si se hubiera movido una hora con esa misma velocidad, hubiera recorrido 90 km.
Ahora bien, es de esperar que el automóvil no se haya movido todo el tiempo con la misma velocidad, pudo ocurrir que el automóvil se haya detenido por algún tiempo (velocidad cero) o, incluso, que se haya detenido y, enseguida, tomado el camino en el sentido opuesto al que llevaba originalmente (velocidad negativa), haciendo esto durante algún tiempo, antes de retomar el sentido original del viaje.
Podemos preguntarnos entonces sobre la manera en la que se movió el automóvil de una ciudad a otra, minuto a minuto, o segundo a segundo, lo que nos lleva a la necesidad de conocer la posición del automóvil en cualquier momento, es decir la función de posición , donde sería el tiempo (medido, por ejemplo, en minutos o en horas) a partir del momento en el que el automóvil partió de la primera ciudad, y sería la distancia (muy probablemente medida en kilómetros) a la que se encuentra el automóvil del punto de partida.
Pues bien, la idea de la velocidad instantánea resulta de considerar un momento dado y otro infinitamente próximo al primero, midiendo entonces la razón entre los cambios instantáneos de la posición y el tiempo, es decir, entre sus diferenciales.
Aproximación polinómica
Este documento trata sobre el desarrollo en serie de potencias de las funciones trascendentes. Antecedentes importantes de estos conceptos los encontramos a mediados del siglo XVIII, en la Introducción al Análisis de los Infinitos, (Introductio in Anaysin Infinitorum, 1748) del genial matemático Leonhard Euler, en donde define (y clasifica) las funciones trascendentes que seguimos usando hasta hoy en día, y obtiene su desarrollo en serie.
En aquella época, uno de los principales usos del desarrollo en serie de potencias era la evaluación de alguna de esas funciones, para un valor dado de la variable, recurriendo, para ello, a un polinomio aproximante, obtenido al truncar la serie. Actualmente, eso ya no es un problema de gran interés, ya que contamos con diversos instrumentos de cálculo que proporcionan el valor de una función con gran precisión y “al instante”.
Sin embargo, la idea de polinomio aproximante es algo que sigue siendo importante, en procesos de modelación, en particular cuando se desconoce la regla de correspondencia de la función, pero se conoce el valor de la función, así como el de su derivada y, eventualmente, el de su derivada segunda, todo ello, para un mismo valor de la variable.
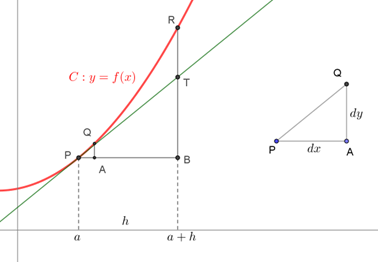
Archivo PW_6A Aproximación polinómica.pdf
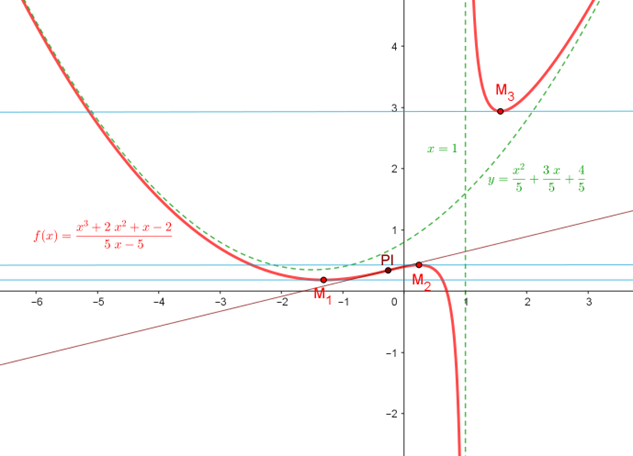
Graficación con Cálculo Diferencial
Anteriormente se han estudiado algunos conceptos que pueden utilizarse para describir gráficamente el comportamiento de una función, partiendo de su regla de correspondencia; por ejemplo, las asíntotas de la función describen el comportamiento de esta para valores grandes de la variable, también se consideraron las funciones definidas mediante cocientes, poniendo atención en los valores de la variable en los que el denominador se anula.
Aquí se retoma el asunto del trazado de la gráfica de las funciones, considerando aquella información que se puede obtener a partir de las funciones derivada primera y derivada segunda, de la función dada.
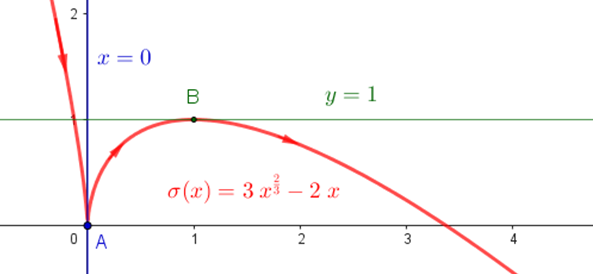
PW_6B-Graficacion-con-ayuda-del-calculo-diferencial.pdf
Puntos estacionarios y valores extremos
En algunos problemas de interés, en las ciencias de la ingeniería, se tiene la necesidad de describir el comportamiento” de una función, conforme se recorre el valor de la variable (de izquierda a derecha), identificando cuando la función crece o decrece, cuando la tangente a la gráfica de la función es horizontal (paralela al eje de abscisas) o vertical (paralela al eje de ordenadas), o cuando la gráfica presenta una concavidad hacia arriba (o hacia abajo), luego de lo cual se pueden encontrar los valores de la variable para los cuales la función tiene un valor extremo (máximo o mínimo), o bien un punto de inflexión, que es dónde la gráfica cambia su sentido de concavidad. De eso trata este documento.