Operación de integración
Se ha estudiado el Cálculo diferencial, cuyo principio básico radica en observar los objetos, no en su totalidad sino más bien a través de una parte infinitamente pequeña de estos. Más específicamente, como lo haría Newton, considerando que las cantidades manifiestan su variación con el paso del tiempo, podemos observar la variación de cada cantidad en un intervalo infinitamente pequeño de tiempo y comparar dos de estas variaciones entre sí.
La operación básica fue entonces la de la diferenciación, es decir, el cálculo de la diferencial, la cual se definió como la variación infinitamente pequeña de una cantidad variable, pero que también la podemos considerar como una parte infinitamente pequeña de una cantidad variable. Aquí se aborda, algo así como “el camino de regreso”; es decir, vamos a ver cómo recuperar el valor de la cantidad entera, a partir del conocimiento de una parte infinitamente pequeña de la misma, a la que se denomina elemento.
PW_7-Operacion-de-Integracion.pdf
Proceso de integración y área bajo la curva
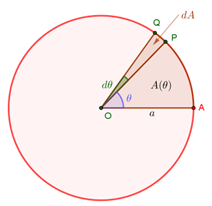
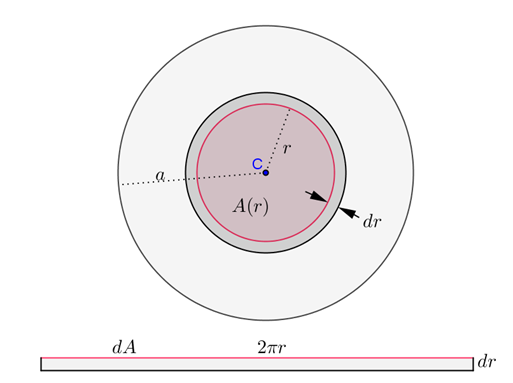
Se ha visto que la operación de integración es la inversa de la diferenciación. Ahora se atenderá el proceso de integración, el cual es de suma importancia en el estudio de las ciencias básicas y de la ingeniería.
Supongamos que el valor de una cantidad depende del valor de una variable
, es decir
es una función de
, y que la cantidad
se genera conforme
cambia su valor de
a
, de manera que
y
, es decir, la cantidad a medir se genera desde cero hasta su valor total, conforme la variable recorre un cierto intervalo.
Supuesto lo anterior, si además se puede establecer que, cuando tiene un incremento infinitesimal
la correspondiente variación de
se puede expresar mediante
, entonces
se podrá obtener al calcular la integral de
.
 |  |
PW_8-Integral-definida-y-area-bajo-la-curva.pdf
Cálculo de cantidades geométricas mediante el Cálculo Integral
En este documento vamos a ver cómo calcular algunas cantidades geométricas, relacionadas con objetos de una, dos y tres dimensiones. Específicamente, se verá cómo calcular la longitud de un arco de una curva, el área de una superficie plana y el volumen de un sólido de revolución, recurriendo, en cualquier caso, al proceso de integración, y considerando la variación de una sola variable.
 |  |
PW_9-Calculo-de-cantidades-geometricas-mediante-el-Calculo-Integral.pdf
