Hablando de lo Infinitesimal
En este documento se atienden algunos de los conceptos que sirven de base en el Cálculo, comenzando con lo relativo a la terminología infinitesimalista, la cual se desprende de dos ideas básicas, una de ellas, de carácter aritmético – algebraico, se refiere a la manera en cómo se realizan operaciones aritméticas entre cantidades de distinto “orden de magnitud”. Ello permite, entre otras cosas, despreciar uno de los términos de una suma cuando dicho término se considera de magnitud infinitamente pequeña respecto de los otros.
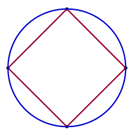
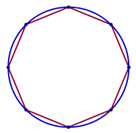
La otra, de carácter geométrico, tiene que ver con la manera en la que vemos una “porción infinitamente pequeña de un objeto”. Esto nos permite, por ejemplo, considerar una circunferencia como un polígono regular con un número infinito de lados, cada uno de ellos de longitud infinitamente pequeña, o, en general, cualquier otra curva como una poligonal con un número infinito de lados, cada uno de ellos de longitud infinitamente pequeña.
 |  |  |  |
PW1_Hablando de lo infinitesimal (PDF)
Aproximación y graficación
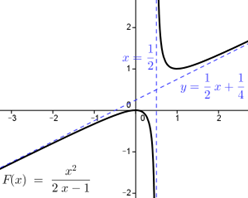
Aquí se presentan dos conceptos importantes en el Cálculo, primeramente, el de la aproximación de una función por medio de un polinomio, que nos permite varias cosas, como evaluar la función haciendo únicamente adiciones y multiplicaciones, utilizar un polinomio en lugar de la función para analizar el comportamiento de esta, al menos en algún intervalo, o introducir al estudiante al concepto de convergencia. Por otra parte, en el estudio de las Ciencias, cuando se analiza la relación entre dos variables, esta puede describirse de varias maneras, por ejemplo, verbalmente (con palabras), algebraicamente (utilizando símbolos), o geométricamente, por medio de una gráfica. Incluso puede hacerse una descripción aritmética, por medio de una tabla mostrando un conjunto de pares ordenados que corresponden a valores de las variables en cuestión. Además, será importante ser capaz de “traducir” de cualquiera de estos lenguajes (verbal, simbólico, gráfico o numérico) al otro, situación que tal vez pudo haberse comenzado a estudiar en el bachillerato, en un curso de Geometría Analítica. Así pues, en este documento se abordarán algunos aspectos de la graficación de funciones, particularmente a la identificación y ubicación de asíntotas o huecos (en lugar de puntos).
 |  |
