Arcos, I. (2019)
Una presentación de los conceptos del cálculo, en escuelas de ingeniería, no centrada en la definición de límite
El Cálculo y su Enseñanza, Enseñanza de las Ciencias y la Matemática. Volumen 12. Enero – Junio 2019. Cinvestav-IPN © Ciudad de México. ISSN 2007-4107. P.p. 46 – 59.
Resumen. Si se admite que la presentación de conceptos matemáticos en la enseñanza debe considerar las necesidades e intereses de aquellos a quienes se dirige el proceso educativo, entonces los cursos de matemáticas que se imparten en las escuelas de ingeniería deben pensarse e impartirse en consideración de la manera en la que los conceptos matemáticos involucrados habrán de ser utilizados en la actividad profesional del ingeniero y, claro está, en la manera en esos conceptos se utilizan para adquirir y utilizar los conocimientos propios de las ciencias de la ingeniería. La presentación tradicional del Cálculo está centrada en el concepto de límite, a pesar de que la experiencia en las aulas muestra claramente que se tienen grandes dificultades para el aprendizaje y a pesar de que los textos utilizados para la enseñanza de las ciencias de la ingeniería utilicen los conceptos del Cálculo con un escaso recurso del concepto de límite. En este documento se pretende insistir en la posibilidad de ofrecer una presentación del Cálculo, en escuelas de ingeniería, que no ponga en el centro de atención al concepto de límite.
DOI: https://doi.org/10.61174/recacym.v12i1.33
Arcos, I. (2024).
Algunas razones por las que los cursos de Cálculo dirigidos a estudiantes de ingeniería deben dejar de centrarse en el concepto de límite (FIME Cap. 2)
Libro completo en:
Marzo 2024
El Cálculo, en las versiones originales de Leibniz o Newton, surgió a fines del siglo XVII, cuando conceptos como los de número real, función, límite o continuidad no eran conocidos, mucho me-nos con el rigor con el que se definen desde hace un siglo. Esas versiones, apuntaladas a lo largo del siglo XVIII, por personajes como Euler, fueron utilizadas en el estudio y la solución de innume-rables problemas de ingeniería, y aún hoy, siguen utilizándose, con algunas “actualizaciones” en la modelación y solución de problemas en el contexto de las Ciencias de la Ingeniería. Entonces, ¿por qué en los textos utilizados para la enseñanza del Cálculo, en las escuelas de ingeniería dejaron de ser versiones válidas, siendo sustituidas por la versión del Cálculo que surgió a partir de los trabajos de Cauchy, a principios del siglo XIX?
Arcos, I., Sepúlveda, D. (2012).
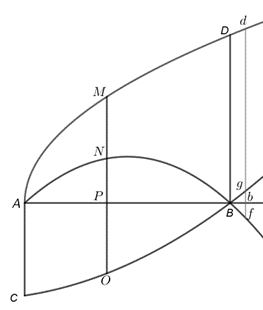
La diferencial de área. Una perspectiva infinitesimalista
Arcos Quezada, J. I., & Sepúlveda Jáuregui, . D. I. (2012). La diferencial de área. Una perspectiva infinitesimalista. El cálculo Y Su enseñanza, 3(1), 35–60.
DOI: https://doi.org/10.61174/recacym.v3i1.137
Diciembre 2012
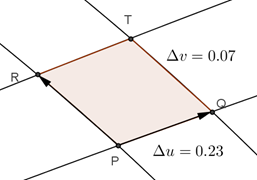
Resumen. En un curso tradicional de cálculo, en escuelas de ingeniería, el concepto de integración se introduce generalmente a partir de sumas de Riemann. Luego, al abordar el asunto de la integral doble o integral de área, se vuelve a recurrir a sumas de Riemann sobre una región inicialmente rectangular, dando lugar a la así denominada integral iterada, en la que “aparece” en el integrando, ya sea dy dx o dx dy, pero no se indica que se trate del producto de las diferenciales de las variables. Esta y otras situaciones en la forma de presentar la integral doble provoca que el estudiante generalmente termine por mecanizar el cálculo de una integral “doble” (y después de la “triple”), sin tener una idea clara sobre lo que se está haciendo y sobre el significado geométrico de esa “dA”. Si se aceptaran los infinitesimales más o menos de la manera en la que fueron concebidos por Leibniz y sus seguidores, el asunto se simplificaría considerablemente, sobre todo si tomamos en cuenta la disponibilidad de un software libre como geogebra, el cual puede utilizarse para hacer una argumentación visual.
|  |
Arcos, I. (2004).
Rigor o entendimiento, un viejo dilema en la enseñanza de las matemáticas: el caso del cálculo infinitesimal
Arcos, I. (2004). Rigor o entendimiento, un viejo dilema en la enseñanza de las Matemáticas: el caso del cálculo infinitesimal. Tiempo de Educar, vol. 5, núm. 10, julio-diciembre, 2004, pp. 77-110 Universidad Autónoma del Estado de México Toluca, México
https://www.redalyc.org/pdf/311/31101004.pdf
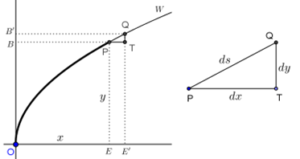
Resumen. El Cálculo infinitesimal, en particular el desarrollado por Leibniz y sus seguidores, a fines del siglo XVII, mostró ser una herramienta sumamente poderosa para la modelación de fenómenos naturales y, por lo tanto, para facilitar el desarrollo de otras ciencias, situación que aún hoy puede apreciarse en textos de ciencias básicas y de la ingeniería. Sin embargo, a partir de la primera mitad del siglo XIX, y como producto de continuos señalamientos sobre una supuesta falta de rigor, el Cálculo infinitesimal fue sustituido gradualmente por la propuesta de Cauchy, que es la que, con algunas modificaciones, se enseña actualmente en las aulas. Esta sustitución ha tenido efectos negativos en el aprendizaje, que, sin embargo, podrían revertirse si se recuperara, al menos parcialmente, el cálculo infinitesimal leibniziano.
Arcos, I. (2022).
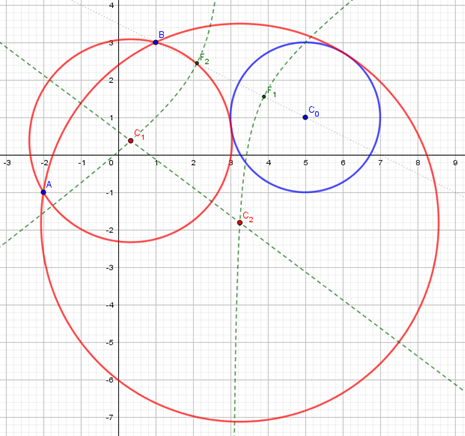
El problema de Apolonio en un contexto escolar y con ayuda de GeoGebra. Investigación e Innovación en Matemática Educativa (2022). Volumen 7
https://revistaiime.org/index.php/IIME/article/view/140/79
Octubre 2022
Resumen. El llamado problema de Apolonio es uno de los problemas de construcción geométrica que más ha atraído la atención de los matemáticos desde que fue enunciado en el siglo III a.C. Sin embargo, debido a la cantidad y complejidad de los conceptos geométricos requeridos para su solución, particularmente si se quiere cumplir con el requisito de utilizar sólo regla y compás, sólo dos de los diez posibles casos del problema pueden ser abordados en la matemática escolar. En este documento se expone una manera de abordar y resolver los distintos casos en una situación escolar, en bachillerato o un programa académico de ingeniería, utilizando para ello, parábolas, elipses e hipérbolas, además de rectas y circunferencias, y contando con la ayuda de GeoGebra